1.4.1 用空间向量研究直线、平面的位置关系

空间中直线、平面的平行(1)

保亭中学  蔡月妃

一．课程目标

1.能用向量语言表述直线与直线、直线与平面的平行关系.

2.能用向量方法证明空间中直线与直线、直线与平面的平行关系.

二、学科素养

1.数学抽象：直线的方向向量与平面的法向量

2.数学运算：空间向量的坐标运算解决直线与直线、直线与平面的平行关系.

三、教学重难点

1.教学重点：用向量语言表述直线与直线、直线与平面的平行关系.

2.教学难点：用向量方法证明空间中直线与直线、直线与平面的平行关系.

四、教学过程

1、复习回顾

利用待定系数法求平面的法向量的步骤：

(1)设向量：设平面的法向量为n=(x,y,z).

(2)找向量：找出(求出)平面内的两个不共线的向量的坐标a=(a1,b1,c1),b=(a2,b2,c2).

(3)列方程：根据法向量的定义建立关于x,y,z的方程组

(4)解方程:解方程组,取其中的一个解,即得法向量.

2、新知探究

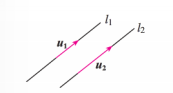（1）思考 1：如何用直线的方向向量表示直线的平行？

设μ1,μ2分别是直线l1,l2的方向向量,

则l1∥l2⇔μ1∥μ2⇔∃λ∈R,使得μ1=λμ2.

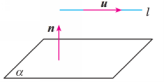（2）思考2：如何用直线的方向向量、平面的法向量来表示直线与平面平行？

设μ是直线l的方向向量,n是平面α的法向量,l⊄α,

则l∥α⇔μ⊥n⇔μ·n=0.

空间中直线、平面平行的向量表示 ：

3、小试牛刀

（1）若两条直线的方向向量分别是a=(2,4,-5),b=(-6,x,y),且两条直线平行,则x=　  ,y=　   . 

答案:-12；15

（2）若直线,且的方向向量为（2,m,1）,平面的法向量为,

则m为（）

A.-4            B.6           C.-8        D.8

答案:C

4、典例解析

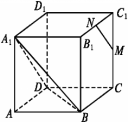例.如图,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.

证明：以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系Dxyz,如图.设正方体的棱长为1,则可求得

M,N,D(0,0,0),A1(1,0,1),B(1,1,0).

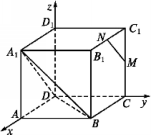于是=(1,0,1),=(1,1,0).

设平面A1BD的法向量为n=(x,y,z),

则

取x=1,得y=-1,z=-1,∴n=(1,-1,-1).

∵·n=·(1,-1,-1)=0,∴⊥n.

又∵MN⊄平面A1BD,∴MN∥平面A1BD.

5.变式训练

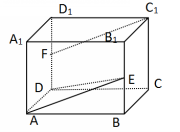
1.已知正方体ABCD-A1B1C1D1的棱长为2，E、F分别是BB1、DD1的中点，求证：FC1∥平面ADE；

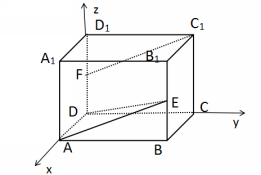证明:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则有D(0,0,0)，A(2,0,0)，E(2,2,1)，F(0,0,1)，C1(0,2,2)，

.

，

,

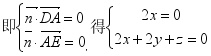6.归纳总结

（1）利用空间向量证明线与线平行的方法：

要证明两直线平行,可先求出两直线的方向向量,然后证明两直线的方向向量共线,从而证明两直线平行.

（2）利用空间法向量的方法证明线面平行方法：

要证明直线与平面平行，先求出直线的方向向量与平面的法向量,证明方向向量与法向量垂直,从而证明直线与平面平行.

7.课后作业

课本31页练习题第3题.

8.教学反思

课堂练习留给学生练习的时间比较少，自己讲的太多，不能够发挥学生的主观能动性。

注意在探究问题时留给学生充分的时间， 使数学教学成为数学活动的教学。从而发展学生的直观想象、逻辑推理、数学建模的核心素养。