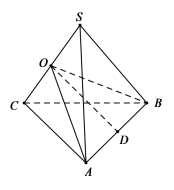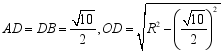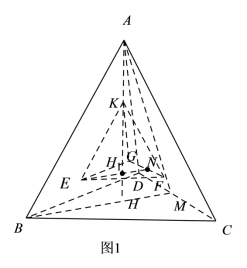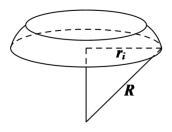球的切接问题

一、知识点总结

1．球的表面积和体积公式

球体的体积公式：，球的表面积公式：．

2．球的切、接问题的一些结论

1）若正方体的棱长为，则正方体的内切球半径是；正方体的外接球半径是；与正方体所有棱相切的球的半径是．

2）若长方体的长、宽、高分别为，，，则长方体的外接球半径是．

3）若正四面体的棱长为，则正四面体的内切球半径是；正四面体的外接球半径是；与正四面体所有棱相切的球的半径是．

4）球与圆柱的底面和侧面均相切，则球的直径等于圆柱的高，也等于圆柱底面圆的直径．

5）球与圆台的底面与侧面均相切，则球的直径等于圆台的高．

3常见模型

（1）

对应公式：

（2）

对应公式：

（3）

对应公式：

（4）

对应公式：

二、常用方法及典型例题

1一条棱垂直于底面

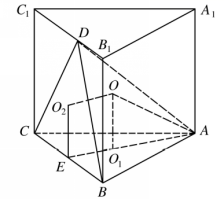
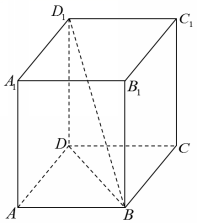
例1《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马.若四棱锥为阳马，垂直于平面，四棱锥的顶点都在球O的球面上，则球O的表面积为（    ）

A．B．C．D．

分析：以为棱把补形成一个长方体，是长方体的对角线，是长方体外接球的直径，也是外接球的直径，由此计算出后可得面积．

解析：是阳马，以为棱补形成一个长方体，如图，则是长方体的对角线，

而是该长方体外接球的直径，也是外接球的直径，

由已知，

球的表面积为．

故选：B．

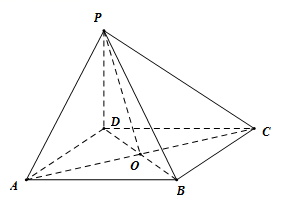
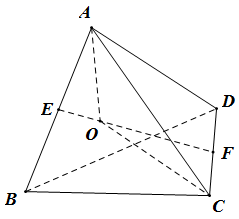
変式练习1．如图，在四棱锥中，底面为菱形，底面，O为对角线与的交点，若，，则三棱锥的外接球表面积为_________．

解析：取中点，中点，连接，则，

因为底面，所以平面，是菱形，则，所以是的外心，

又底面，平面，所以，所以到四点距离相等，即为三棱锥的外接球球心．

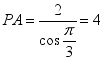又，，所以，所以，

所以三棱锥的外接球表面积为．

故答案为：．

2、对棱相等的三棱锥外接球

例2、一个四面体ABCD的所有棱长都为，四个顶点在同一球面上，则此球的表面积为（    ）

（A）       （B）      （C）          （D）

解：A

変式练习2、四面体ABCD中，已知AB=CD=，AC=BD=，AD=BC=，则四面体ABCD的外接球的表面积为(     )

A．25πB．45πC．50πD．100π

解：C

解析：由题意可采用割补法，考虑到四面体ABCD的四个面为全等的三角形，

所以可在其每个面补上一个以，，为三边的三角形作为底面，且以分别x，y，z长、两两垂直的侧棱的三棱锥，从而可得到一个长、宽、高分别为x，y，z的长方体，并且x2+y2=29，x2+z2=34，y2+z2=37，

则有（2R）2=x2+y2+z2=50（R为球的半径），得R2=，

所以球的表面积为S=4πR2=50π．

3、正棱锥外接球

例3若一个四棱锥底面为正方形, 顶点在底面的射影为正方形的中心, 且该四棱锥的体积为,当其外接球的体积最小时, 它的高为（   ）

A．                 B．                C．               D．

変式练习3正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（ ）

A．B．C．D．

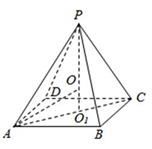解析：正四棱锥P-ABCD的外接球的球心在它的高上，

记为O，PO=AO=R，，=4-R，

在Rt△中，，

由勾股定理得，

∴球的表面积，故选A.

4、墙角型外接球

例4已知、、两两垂直且，，，则过、、、四点的球的体积为________

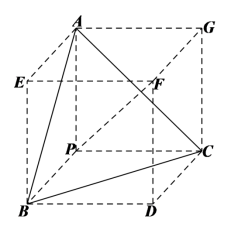解析：将三棱锥补成长方体，计算出长方体的体对角线长，可得出外接球的半径，利用球体体积公式可得结果.

由于、、两两垂直，将三棱锥补成长方体，

则长方体的体对角线长为，

故三棱锥的外接球的半径为，

因此，该球的体积为.

故答案为：.

変式练习4已知长方体的两个底面是边长为的正方形，长方体的一条体对角线与底面成角，则此长方体的外接球表面积为（    ）

A．B．C．D．

解析：记该长方体为，为该长方体的一条体对角线，其与底面所成角为，

因为在长方体中，侧棱底面，

则为与底面所成角，即，

因为长方体的两个底面是边长为的正方形，所以，

则，所以，

又长方体的外接球直径等于其体对角线的长，

即该长方体外接球的直径为，

所以此长方体的外接球表面积为.故选：A.

三、基础训练

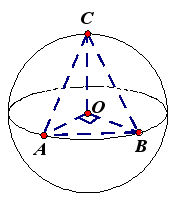
1已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为(     )

A．36π    B.64π    C.144π    D.256π

解析：如图所示，当点C位于垂直于面的直径端点时，三棱锥的体积最大，设球的半径为，此时，故，则球的表面积为，故选C．

2．已知正四棱锥的体积为，侧棱与底面所成的角为，则该正四棱锥外接球的表面积为___________.

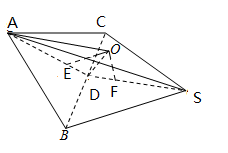
解析：如下图所示，设正四棱锥的底面的中心为，连接、、，

设正四棱锥的底面边长为，则，

由于为正四棱锥的底面的中心，则平面，

由于正四棱锥的侧棱与底面所成的角为，则，

所以，是以为直角的等腰直角三角形，

同理可知，是以为直角的等腰直角三角形，

为的中点，，，

，解得，

，由直角三角形的性质可得，

即，所以，为正四棱锥外接球的球心，

球的半径为，该球的表面积为.

故答案为：.

3在封闭的直三棱柱内有一个体积为V的球，若，，，

，则该球体积V的最大值是

A．B．C．D．

解析：设的内切圆半径为，则，故球的最大半径为，故选B.

考点：球及其性质.

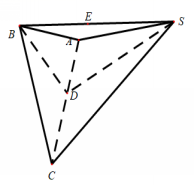
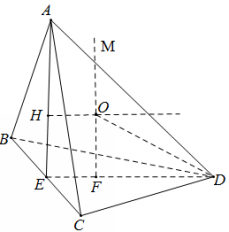
2．（2020·四川泸州市·高三一模）已知三棱锥中，和是边长为2的等边三角形，且平面平面，该三棱锥外接球的表面积为（    ）

A．B．C．D．

解析：取的中点，连接，则，

因为平面平面，所以可证得平面，平面，

取的外心，作，则四点共面，

取的外心，过点作的平行线交于点，

因为垂直平面，则平面，

所以点到四点的距离相等，所以点为三棱锥外接球的球心，

连接，可求得，所以，所以外接球的表面积为.

故选：D.

四、能力提升

一、单选题

1．在三棱锥中，若该三棱锥的体积为，则三棱锥外球的体积为（    ）

A．B．C．D．

2．《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马.若四棱锥为阳马，垂直于平面，四棱锥的顶点都在球O的球面上，则球O的表面积为（    ）

A．B．C．D．

3．四个半径为2的球刚好装进一个正四面体容器内，此时正四面体各面与球相切，则这个正四面体外接球的表面积为（    ）

A．B．

C．D．

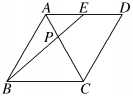
4．已知在正四面体ABCD中，E是AD的中点，P是棱AC上的一动点，BP＋PE的最小值为，则该四面体内切球的体积为（    ）

A．πB．π

C．4πD．π

5．在三棱锥中，，，，二面角的余弦值是，若都在同一球面上，则该球的表面积是（    ）

A．B．C．D．

第II卷（非选择题）

请点击修改第II卷的文字说明

二、填空题

6．已知三棱锥，分别是棱的中点，且，则此三棱锥外接球的表面积_________.

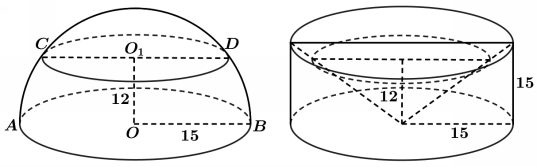
7．如图，有一个半径为的半球，过球心作底面的垂线，上一点满足，过作平行于底面的截面将半球分成两个几何体，其中较大部分的体积为_____________.

8．已知直三棱柱中，，点在棱上且满足则三棱锥的外接球的表面积为________________________．

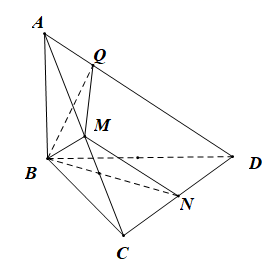
9．已知三棱锥的各顶点都在球O上，点M，N分别是，的中点，上平面，，，则下列结论正确的是___________.

①平面；

②球O的体积是；

③二面角的余弦值是；

④平面被球O所截的截面面积是

10．在三棱锥中，，二面角为，则三棱锥的外接球的表面积为______________.

参考答案

1．D

【分析】

设SC的中点为O，AB的中点为D，连接OA、OB、OD，根据，得到 ，则O为其外接球的球心，易证平面AOB，由，求得半径即可.

【详解】

如图所示：

设SC的中点为O，AB的中点为D，连接OA、OB、OD，

因为，

所以,

则，

所以O为其外接球的球心，设球的半径为R，

因为，，

所以，

所以，

因为，

所以平面AOB，

所以，

解得，

所以其外接球的体积为，

故选：D

2．B

【分析】

以为棱把补形成一个长方体，是长方体的对角线，是长方体外接球的直径，也是外接球的直径，由此计算出后可得面积．

【详解】

是阳马，以为棱补形成一个长方体，如图，则是长方体的对角线，

而是该长方体外接球的直径，也是外接球的直径，

由已知，

球的表面积为．

故选：B．

3．A

【分析】

画出直观图，梳理条件，再画出截面图，从中找到等量关系，求出外接球半径，从而求出外接球的表面积.

【详解】

如图1所示，正四面体ABCD中，AH⊥底面BCD，E、F、G、K为四个球的球心，M为CD中点，连接BM，AM，易知B、H、M三点共线，直线AH交平面EFG于点，连接，交GF于点N，则N为GF的中点，因为内切球半径为2，故EF=4，画出截面ABM如图2所示，正四棱锥EFGK外接球球心设为O，则正四面体ABCD的外接球球心与正四面体EFGK外接球球心重合，设正四面体ABCD的外接球半径为R，正四面体EFGK外接球半径为r，在图2中，EK=4，，，，所以

由，即，解得：

所以

过点E作EP⊥BM于点P，则EP=2

则△BEP∽△

∴，

解得：

∴

∴正四面体ABCD的外接球表面积

故选：A

【点睛】

与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.

4．D

【分析】

首先设正四面体的棱长为，将侧面和沿边展开成平面图形，根据题意得到的最小值为，从而得到，根据等体积转化得到内切球半径，再计算其体积即可.

【详解】

设正四面体的棱长为，将侧面和沿边展开成平面图形，如图所示：

则的最小值为，

解得.

如图所示：为正四面体的高，

，正四面体高.

所以正四面体的体积.

设正四面体内切球的球心为，半径为，如图所示：

则到正四面体四个面的距离相等，都等于，

所以正四面体的体积，解得.

所以内切球的体积.

故选：D

5．C

【分析】

取的中点，连接，易得，利用余弦定理、勾股定理算得，可知，所以为直角三角形，同理可得为直角三角形，取中点，可知为外接球球心，计算的长度即可.

【详解】

取的中点，连接.因为，所以，

可得即为二面角的平面角，故.

在直角中，，同理可得，由余弦定理得，

解得.

在中，，

所以为直角三角形，同理可得为直角三角形，取中点，

则，在与中，，，

所以点为该球的球心，半径为，所以球的表面积为.

故选：C

【点睛】

本题主要考查三棱锥外接球的体积的计算，考查学生空间想象能力与数学运算能力，是一道中档题.

6．

【分析】

由已知得出是，的中垂线，在取点，使得时列出方程求出的位置，即可求出外接球半径，进而求出外接球表面积.

【详解】

解：在上取一点，连接，，如下图所示

分别是棱的中点，且

是，的中垂线

，

外接球球心到各顶点的距离相等

只需要即可满足，此时为外接球球心

设，则，

令，即

解得：

即外接球半径

三棱锥外接球的表面积为

故答案为：.

7．

【分析】

利用祖暅原理计算出截面以上部分的体积，再利用半球的体积减去截面以上部分的体积可得结果.

【详解】

设截面以上部分的体积为，截面以下部分的体积为，

设，，则，，

将进行等分，过这些等分点作平行于底面的平面，将截面以上部分切割成层，

每一层都是近似于圆柱形状的“小圆柱”，

这些“小圆片”的体积之和即为，

由于“小圆片”近似于圆柱形状，所以它的体积也近似于相应圆柱的体积，

它的高就是“小圆片”的厚度，底面就是“小圆片”的下底面，

由勾股定理可知第层（由下向上数）“小圆片”的下底面半径为，

于是，第层“小圆片”的体积为，

所以，

，

所以，，

故.

故答案为：.

8．

【分析】

设和的外接圆圆心分别为，过作与平面垂直的直线，过作与平面垂直的直线，两直线交点为外接球球心，由此求得球半径得表面积．

【详解】

设和的外接圆圆心分别为，外接圆半径分别为，

三棱锥的外接球的球心为．

因为平面平面所以三棱锥的外接球球心在过点且与平面和平面垂直的两条直线的交点上．

因为，即是等边三角形，故．

设点是的中点，连接在上，

利用平面几何知识易求得

由余弦定理得，所以

由正弦定理得

又，在中，

即三棱锥的外接球的半径，从而外接球的表面积为．

故答案为：

9．①②

【分析】

对①，利用判定定理判断；对②，找到球心，得到半径，最后计算；对③，过点作，找到二面角的平面角，然后计算即可；对④，利用等体积法计算.

【详解】

如图：

对于选项①，因为平面，所以，

由，，可得，

满足，所以，又，

所以平面，故①正确；

对于选项②，是和的公共斜边，

所以的中点即三棱锥外接球的球心，

所以球的半径为，球的体积为，故②正确；

对于选项③，过点作，垂足为，连接，易证平面，

所以，又，所以平面，所以，

所以为二面角的平面角，在中，可得，

在中，可得，在中，，

则 ，故③错误；

对于选项④，设到平面的距离为，

平面被球所截的截面圆的半径为，因为是的中位线，

所以到平面的距离等于到平面的距离，

故，即，得，

所以，所以截面圆的面积为，故④错误.

故答案为：①②

10．##

【分析】

取线段的中点，连结，，由题意得，，是二面角的平面角，，由以上垂直关系得平面，分别取，的三等分点，，在平面内，过点，分别作直线垂直于，，两条直线的交点即球心，连结，则球半径，由此能求出球的表面积．

【详解】

取线段的中点，连结，，由题意得，，

是二面角的平面角，，

由以上垂直关系可得平面，分别取，的三等分点，，

在平面内，过点，分别作直线垂直于，，两条直线的交点即球心，

连结，则球半径，

由题意知，，，，

连结，在中，，，

，

球的表面积为．

故答案为：．