2022年春季八年级数学期中达标检测题
时间：100分钟 内容：第16-18章 满分120分
题 号 | 一 | 二 | 三 | 总分 |
得 分 |
|
|
|
|
一、选择题（本答题满分36分，每小题3分）
1、 （ ）
A． B. C. D.
2、下列二次根式中，属于最简二次根式的是 （ ）
A. B. C. D.
3、下列各组数中，不能构成直角三角形的是（ ）
A．1， ， B．3，4，5 C．5，12，13 D．4， ，5
4、下列二次根式中，不能与 合并的是（ ）
A. B. C. D.
5、下列计算正确的为（ ）
A. B. C. D.
6、在Rt△ABC中，∠C=90°，且AC=3cm，AB=4cm，则BC的长为（ ）
A．5cm B．4cm C． D．5cm或
7、下列命题中，正确的是（ ）
A．有一个角是直角的四边形是矩形 B．对角线互相平分且垂直的四边形是菱形
C．两组邻角相等的四边形是平行四边形 D．对角线互相垂直且相等的四边形是正方形
8、如图1，在平面直角坐标系中，∠AOP=30°，PA＝2，则P点的坐标为( )
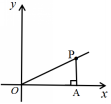
A．( 2，4) B．( 4，2) C．（2， ） D．( ，2 )
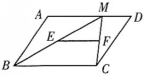
9、如图2，在平行四边形ABCD中，∠B=80°，AE平分∠BAD交BC于点E，CF∥AE交AD于点F，则∠1=（ ）
A．40° B．50° C．60° D．80°
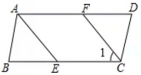
10、如图3，在□ABCD中，M为边AD上一点，E、F分别是BM，CM的中点，若EF=6，则AD的长为（ ）
A．3 B．6 C．12 D．18
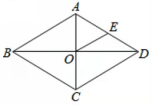
11、如图4，在菱形ABCD中，对角线AC、BD交于点O，E为AD边的中点，BD=8,AC=6，则OE的长为 （ ）
A． B． C． D．2
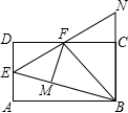
12、如图5，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，将△DEF沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N．有下列四个结论：①DF＝CF；
②BF⊥EN；③△BEN是等边三角形；④S△BEF＝3S△DEF．其中正确的是（ ）
A．①②③ B．①②④ C．②③④ D．①②③④
二、填空题（本答题满分16分，每小题4分）
13、计算 .
14、“平行四边形的对角线互相平分”的逆命题是 ，此逆命题是____命题（真、假）
15、已知菱形的边长和一条对角线的长度均为2cm，则菱形的面积为
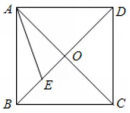
16、如图6，正方形ABCD的对角线AC，BD交于点O，AE平分∠BAC交BD于点E，若OA=1，则BE的长为
三、解答题（本题满分68分）
17、计算（每小题5分，共10分）
（1） （2）
18、（10分）
（1） （2）
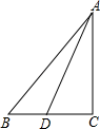
19、（10分）如图，在△ADC中，AD＝15，AC＝12，DC＝9，点B是CD延长线上一点，连接AB，若AB＝20．求BD的长．
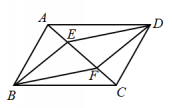
20、（10分）如图，E、F是□ABCD对角线AC上的两点，AE=CF.
求证：BE＝DF.
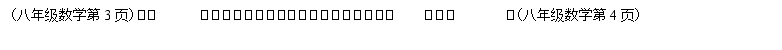
21、（14分）如图，在矩形ABCD中，AB=4，BC=3，过对角线BD的中点O的直线分别交AB、CD边于点E、F．
（1）求证：四边形BEDF是平行四边形；
（2）当四边形BEDF是菱形时，求EF的长．
22、（14分）如图，已知四边形ABCD为正方形，点E为对角线AC上的一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE，EF为邻边作矩形DEFG，连接CG.
（1）求证：矩形DEFG是正方形；
（2）
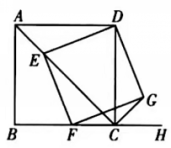判断CE,CG与AB之间的数量关系，并给出证明.