2024年秋季九年级数学期中达标检测题

时间：100分钟     内容：九年级（21-23章）     满分120分

一、选择题（本答题满分36分，每小题3分）

1．下列是一元二次方程的是（  ）

A．    B．C．   D．

2．下列函数中，图像是一条抛物线的是（   ）

A．B．C．D．

3．下列图形中，既是轴对称图形又是中心对称图形的是（   ）

A．平行四边      B．正三角形       C．菱形     D．等腰三角形

4．用配方法解方程x2-2x=3时，配方后正确的是（　　）

A．  B．C．D．

5．临高教育局要组织一次篮球联赛，赛制为单循环（每两队都赛一场），计划安排36场比赛，则参加比赛的球队有（     ）支

A．7           B.8C.9D.10

6．方程的        解是（  ）

A．    B．C．     ，D．，

7．若二次函数的图像经过点，则该图像必经过点（  ）

A．B．C．D．

8．下列关于抛物线2+1的说法，正确的是（  ）

A．开口向下B．对称轴是=-1C．顶点为（-1，1）D．有最小值=1

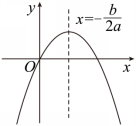
9．二次函数的图象如图所示，则一次函数的图象一定不经过（ ）

A．第一象限B．第二象限C．第三象限    D．第四象限

10．已知二次函数和（m是常数）的图象与x轴都有两个交点，且这四个交点中每相邻两点间的距离都相等，则这两个函数图象对称轴之间的距离为（      ）

A．2B．C．4D．

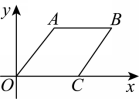
11．如图，菱形的顶点O与原点重合，点C在x轴上，点A的坐标为，将菱形绕点O逆时针旋转，每次旋转，则第次旋转结束时，点B的坐标为（　　）

A．B．C．D．

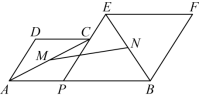
12．如图，已知，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，，M，N分别是对角线AC，BE的中点．当点Р在线段AB上移动时，点MN之间的距离最短为（     ）

A．2B．C．4D．

第9题图                  第11题图                   第12题图

2、填空题（本答题满分12分，每小题3分）

13．若关于的方程的一个根为3，则的值为      ．

14．已知一次函数，若随着的增大而减小，则的值为       。

15．对于一个二次函数（）中存在一点，使得，则称为该抛物线的“开口大小”，那么抛物线y=-x2+2x-2 “开口大小”为          。

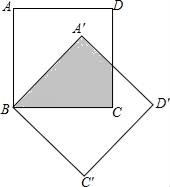
16．如图，将边长为2cm的两个互相重合的正方形纸片按住其中一个不动，另一个绕点B顺时针旋转一个角度α（0°＜α＜90°），若两正方形重叠部分的面积为，则这个旋转角度为     度。

三、解答题（本题满分72分）

17．解方程：（每小题6分，共12分）

(1)；                     (2)．

18.（12分） 为何值时，关于的二次方程．

(1)有两个不等的实数根？

(2)有两个相等的实数根？

(3)无实数根？

19.（10分）已知点，，，根据下列条件分别求a，b的值．

(1)A，B两点关于x轴对称；

(2)A，B两点关于y轴对称；

(3)A，B两点关于坐标原点对称；

(4)轴；

(5)A，B两点在第二，四象限的角平分线上．

20.（10分）临高县某店经销一种建筑材料，当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需成本及其它费用100元．设每吨材料售价为x（元），该经销店的月利润为y（元）。

（1）求出y与x的函数关系式（不要求写出x的取值范围）；

（2）该经销店要获得最大月利润，售价应定为每吨多少元；

21.（12分）如图，已知抛物线 经过两点． 与y轴交于点 C．

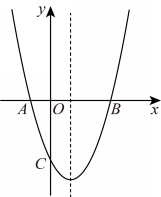(1)求抛物线的解析式；

(2)点P为抛物线上一点，若 求出此时点P的坐标．

(3)在对称轴上是否存在点Q，使△AQC周长最小，若存在，求出点Q坐标和△AQC周长，若不存在，请说明理由。

22.（16分）在△ABC中，，，点在边上，且，将线段绕着点A顺时针旋转，得到线段，连接.

(1)如图，求证：；

(2)如图，过点作交延长线于点，与交于点，探究线段与的数量关系；

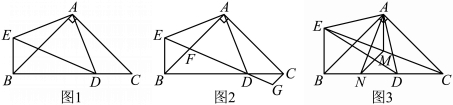
(3)如图，连接，点分别是、的中点，，，请直接写出△AMN的面积。